…und immer wieder die Zeit
Es ist eine Tatsache, das Tontechniker inflationär mit dem Begriff Phase um sich schmeißen um damit Dinge zu umschreiben die meist zwar irgendwas mit dem Thema Zeit zu tun haben aber selten mit dem was grade das Problem ist geschweige denn physikalisch passiert. Der Grund dafür liegt in der weiten Verbreitung von 2-kanaligen Messystemen die uns mittels FFT Dinge anzeigen um unsere Arbeit schneller und präziser zu verrichten. Neben dem oftmals in Vergessenheit geratenen Hören sehen wir nun i.d.R. zwei Informationen, Amplitudenfrequenzgang und Phasenfrequenzgang. Daraus leiten wir beim Einrichten von Beschallungssystemen drei Parametrierungen ab, Filter zur Frequenzgangsgangsoptimierung, Pegelanpassungen und zeitliche Verzögerungen. Darüberhinaus spielen zwar weitere Ableitungen wie Sprachverständlichkeitsmessungen oder sich wiedersprechende Pegelvorschriften wie etwa „Maximalpegel UNBEDINGT unmanipulierbar BlaBlaBla dB“ ABER „zur Evakuierung UNBEDINGT 3x soviel“, diese sollen aber hier keine Rolle spielen. Der Fokus dieses Artikels liegt auf dem Begriff und der Definition von Gruppenlaufzeit. Ziel dieses Beitrages ist es mit Missverständnissen aufzuräumen und eine Abgrenzung zum Begriff Phase und Delay vorzuschlagen. Spätestens wenn man Allpass Filter in seiner Werkzeugkiste zur Systemeinrichtung hat und diese gegenüber einfachen Delays für das Phase Alignement von Top und Sub, oder schlimmer noch Cardioid oder Endfired Arrays benutzt sollte man halbwegs wissen was Gruppenlaufzeit bedeutet und optimaler weise sprechen wir dann bei der Verwendung der Begriffe von dem gleichen physikalischen Phänomen. Mein Dank gilt an dieser Stelle meinen lieben Kollegen Michael Häck, Markus Zehner und Merlijn van Veen die nicht nur den Anstoß gaben mal ernsthaft darüber nachzudenken sondern auch intensiv und kontrovers mit mir diskutierten sowie teilweise auch anderer Auffassung sind. Hier möchte ich meine Auffassung teilen ohne den Anspruch zu erheben das meine Ableitungen die einzig gültigen sind. Im folgenden möchte ich eine Argumentationskette aufbauen die relativ weit vorne anfängt um Missverständnisse ob der Grundlagen auszuschließen und dabei auf alle Parameter zu verzichten die für das Verständnis der Zeitachse, Phase und Gruppenlaufzeit irrelevant sind. Wer der Argumentation nicht folgen möchte weil er sich nicht mit selbstverständlichen Grundlagen auseinandersetzen will, möge zum Fazit vorspulen, dieses Versäumnis jedoch nachholen bevor meine Schlussfolgerungen in der Luft zerrissen werden.
Harmonische Schwingung
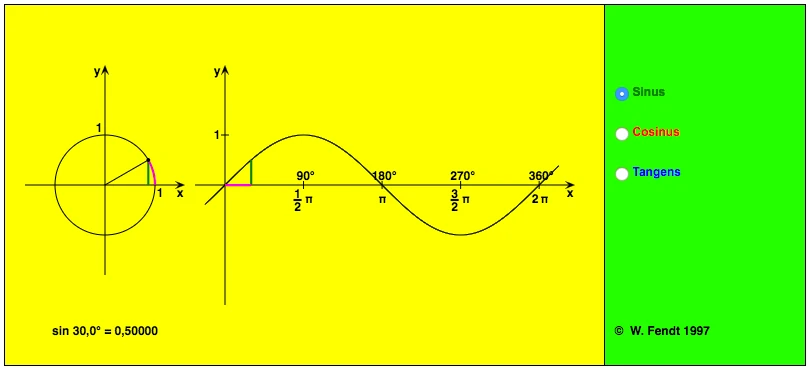
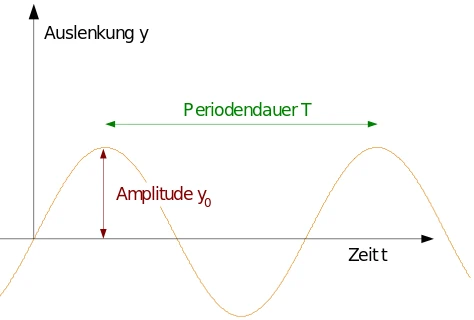
Ein ungedämpftes Federpendel schwingt in einer Sinusfunktion, die Kräfte die in beide Richtungen wirken sind gleich. Der “Zeiger” auf der “Uhr” dreht sich mit konstanter Winkelgeschwindigkeit. Es resultiert eine periodische Schwingung mit der Periodendauer T basierend auf der Winkelgeschwindigkeit des Zeigers. Die Frequenz wird mit ihrem Kehrwert f=1/T beschrieben. Die Position des Zeigers entspricht dem Amplitudenwert der Sinus Schwingung. Der absolute Zeitpunkt t eines Amplitudenwertes entspricht dem relativen Phasenwinkel Phi des Zeigers. Relativ bedeutet, dass die absolute Position des Startwertes des Zeigers Definitionssache ist, so könnte z.B. der Zeiger auf 13:00 starten, pünktlich zur Mittagspause und wir würden definieren das dies die 0 Grad Position ist. …das tuen wir nicht und einigen uns auf die abgebildete Variante basierend auf der Sinusfunktion die ihren Ursprung bei Sin = 0° bei 15:00 hat der Zeiger dreht gegen den Uhrzeigersinn. Folglich hat jeder Zeitpunkt t in der abgebildeten Zeitebene rechts einen dazugehörigen Phasenwinkel. Der Phasenwinkel selbst hat seinen Ursprung in der Geometrie des Kreisausschnittes links, auf die Zeitdomäne ist er nur übertragen.

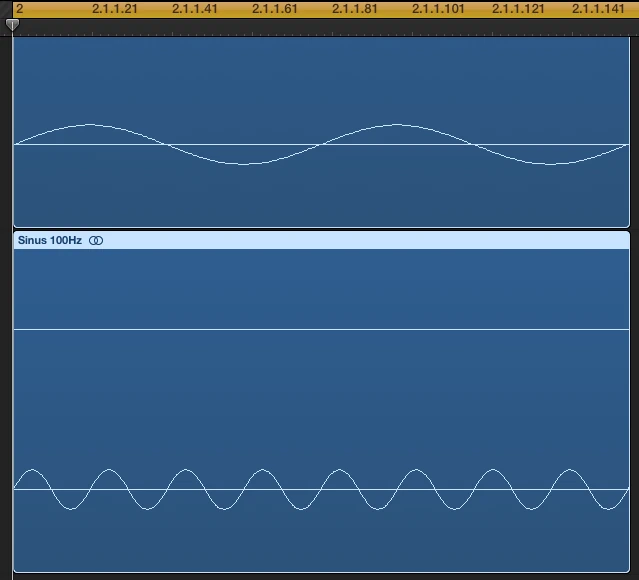
Überlagerung zweier harmonischer Schwingungen
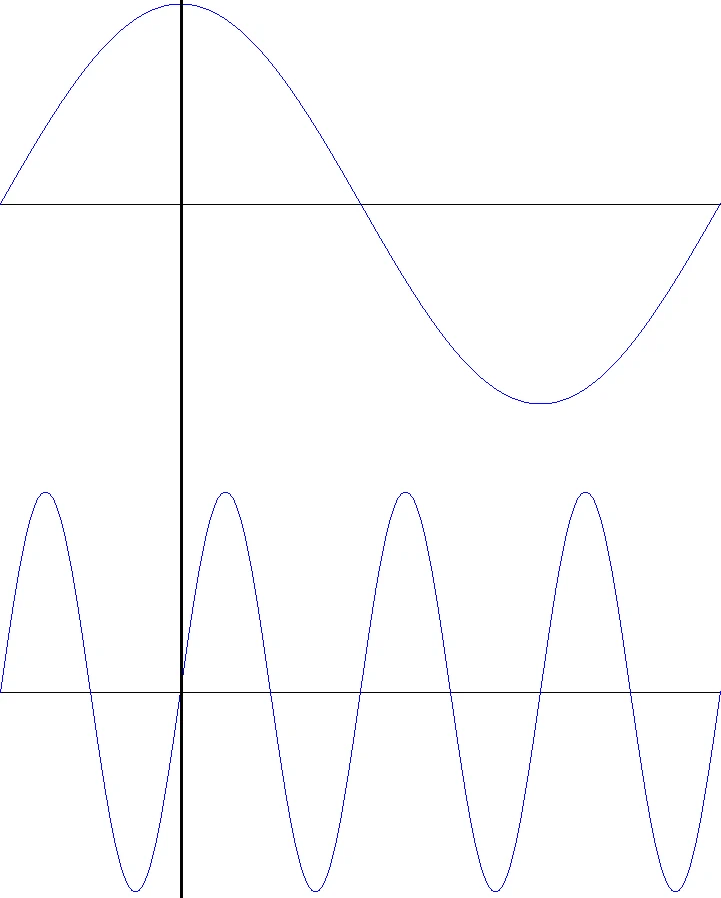
Überlagern sich zwei periodische Schwingungen unterschiedlicher Frequenz gibt es ein Definitionsproblem der Phasenwinkel, denn der Phasenwinkel beschreibt den Zeitpunkt eines Amplitudenwertes einer Schwingung. Ist der Abgebildete Zeitpunkt z.B. 90 Grad oder 360 Grad? Die Antwort lautet: für die niedrigere abgebildete Frequenz 90 Grad (oben) und für die höhere 360 Grad (unten). Das wirft die Frage auf, was ist der Unterschied zwischen 360 Grad und 0 Grad?
Die Antwort ist einfach, 0 Grad ist stets der relative Startpunkt einer Betrachtung, der Startpunkt der Schwingung, von da an wird raufgezählt, für ganzzahlige Periodendauern 360°, 720°, 1440° usw. Das wiederum zeigt uns die Grenzen dieser Betrachtung auf, wer will schon wissen wie viel Grad 5 Minuten 23 Sekunden eines 12,7kHz Sinus ist? …eine völlig unbrauchbare Information! Selbstverständlich addieren sich die überlagerten Schwingungen in der realen Welt und ergeben eine neue Schwingungsform. …und genau das treiben wir jetzt direkt mal auf die Spitze.
Komplexe Schwingungen
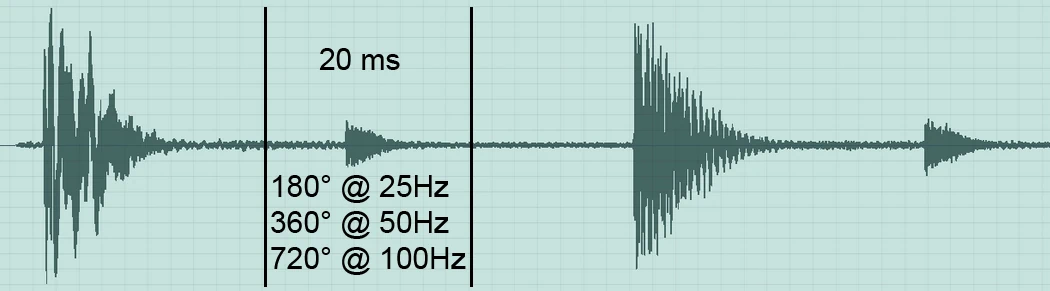
Hier sehen wir eine typische Nichtharmonische Schwingung wie sie Tontechniker hören wenn sie mal die ganzen Dynamik Plug Ins nicht so hart anfahren würden, jeder Periodendurchgang ist individuell und einzigartig anders …es sei denn die Kick Drum ist gesampelt 🙂 Hier gibt es keine Phasenwinkel! Das einzige was man machen kann ist einen Zeitabschnitt zu definieren, ihn in eine Frequenz umzurechnen und zu sagen “das hier sind 360° bei Frequenz X, oder X° bei 100Hz”
Nun spielen wir dieses eine komplexe Signal in ein Übertragungssystem bestehend aus mehreren Komponenten z.B. eine Beschallungsanlage mit L, R, Sub und betrachten mit Hilfe von Messtechnik die Impulsantworten der einzelnen Wege L, R, Sub und deren Ableitungen Phasenfrequenzgang und Amplitudenfrequenzgang. Doch klären wir zunächst was eine Impulsantwort ist.
Impulsantwort

Nehmen wir ein beliebiges Übertragungssystem, in unserem Fall Endstufe 1-3 , mit Lautsprecher 1-3 für L, R Sub. In den Eingang speisen wir einen Dirac-Impuls und am Ausgang ergibt sich eine Impulsantwort die das Übertragungsverhalten vollständig beschreibt. Da ein Dirac-Impuls eine theoretische Konstruktion ist die man nur näherungsweise in die Praxis umsetzen kann und außerdem bei der Messung von Lautsprechersystemen weitere Probleme wie Übersteuerung verursachen würde verwendet man üblicherweise andere Stimuli wie Rosa Rauschen oder Sinus Sweeps und vergleicht einfach das Eingangssignal mit dem Ausgangssignal. Ein Stück Supraleiter als “System” verursacht theoretisch keine Differenz. …wer weiß das schon so genau, das ist ziemlich kalt. Außerdem wissen wir sowieso das unser System eine Differenz aufweist. Ein Lautsprecher ist grundsätzlich mangelhaft. Unsere Fehleinschätzung ist, dass dieser Mangel im Arbeitsbereich konstant ist und korrigiert werden kann. Als Folge setzen wir ihm einen invertierten Fehler vorne an, welchen wir ironischerweise Controller nennen. Das Problem bleibt das gleiche, das Übertragungssystem ist nicht linear, allerdings sind wir in der Lage einzelne Ebenen zu Ungunsten anderer zu linearisieren, so kann z.B. der Amplitudenfrequenzgang mittels Filter optimiert werden, zu Ungunsten des Phasenfrequenzgang oder umgekehrt. Mit FIR Filtern wiederum können wir beides optimieren zu Ungunsten der Systemlaufzeit (d.h. Latenz) und der Impulsantwort (d.h. Vorschwingen) zusätzlich zum ohnehin vorhandenen Nachschwingen der IR Filter. Nehmen wir modellhaft an wir haben ein fehlerhaftes System Lautsprecher, das durch einen Gegenfehler Controller perfekt korrigiert werden kann, so bliebe dennoch eine Systemlaufzeit als Fehler, (Arbeit = Leistung x Zeit …sorry ich bin Elektriker …Physiker sagen Kraft x Weg) Im Grunde spielt es keine Rolle aber wir sollten und bewusst machen, das wir Energie übertragen und nicht einfach nur eine Spannung erzeugen. Die Akustische Energie ist die Ursache die elektrische Energie die Wirkung, diese wiederum die Ursache für akustischen Energie …nur lauter und geiler:) Doch STOP! …Springen wir wieder einen Punkt zurück zum Thema Phase.

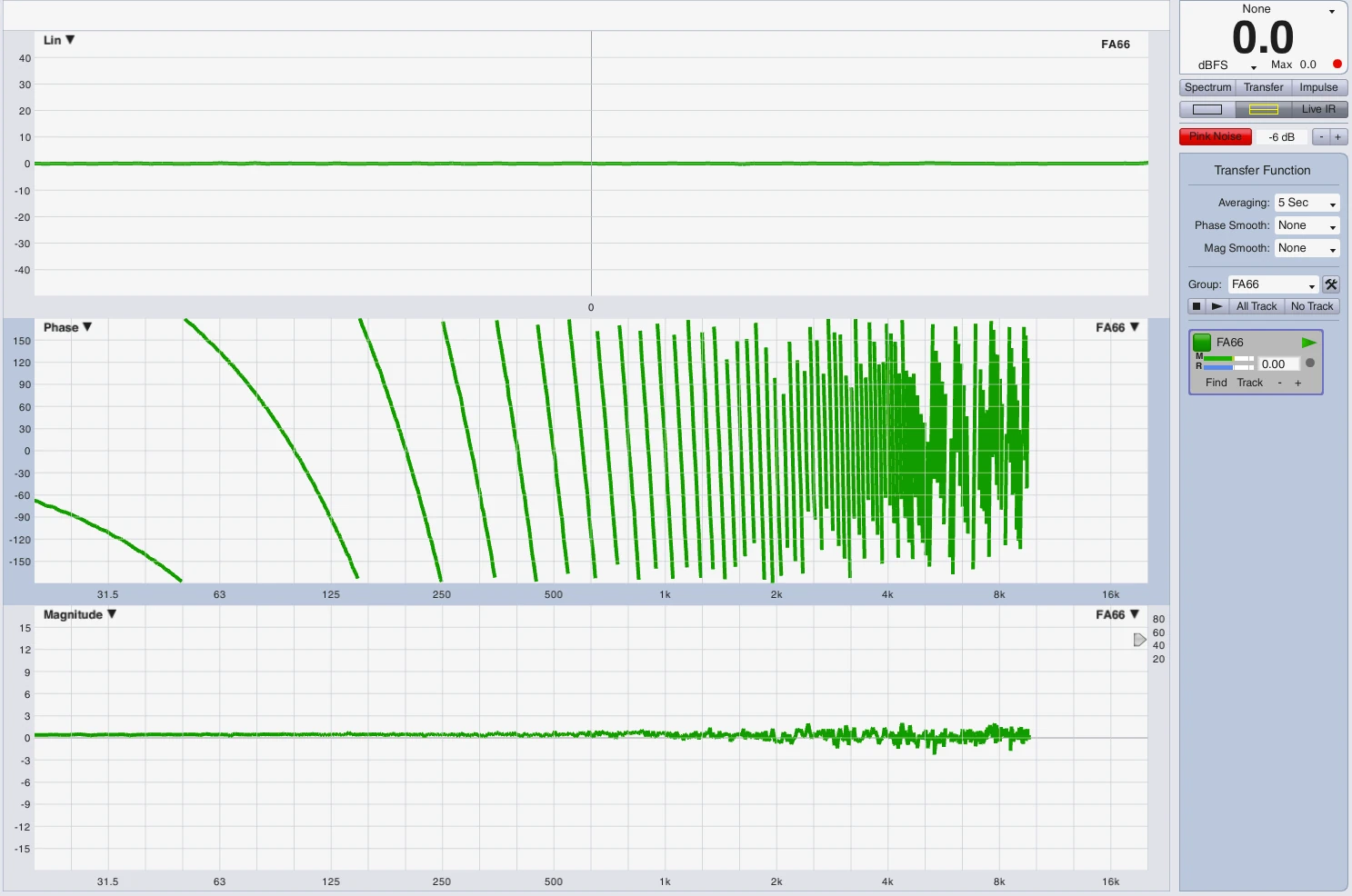
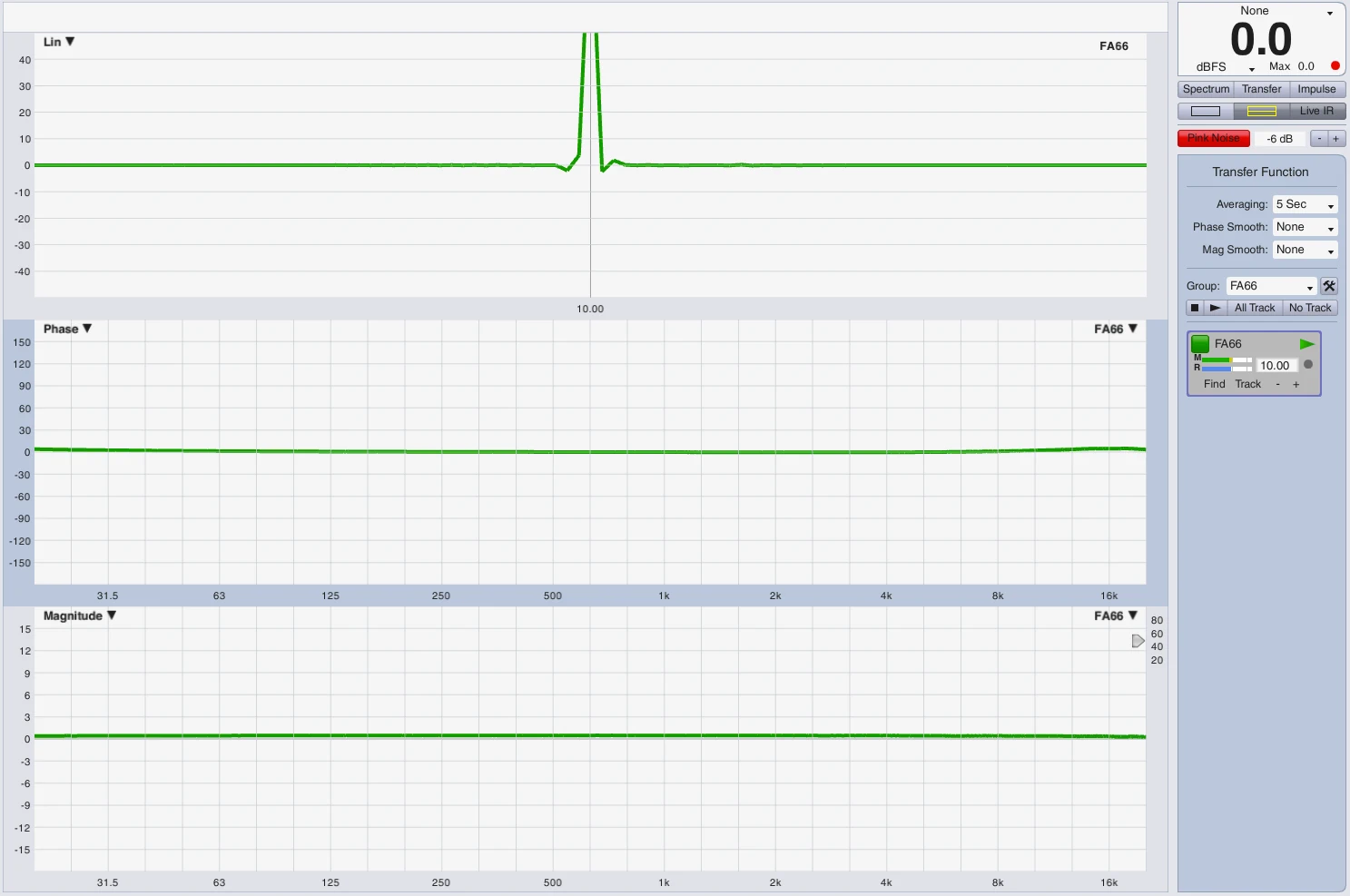
Das oben genutzte Beispiel der komplexen Schwingung liegt am Eingang unserer Beschallungsanlage an und wir vergleichen es mit dem Systemausgang, z.B. Lautsprecher Links an Messmikrofon. Für diese Modellvorstellung nehmen wir mal rein hypothetisch an das, dass System keinerlei Verzerrung aufweist und mit einer konstanten Gruppenlaufzeit lediglich eine Verzögerung X verursacht. Ein Teil dieser Verzögerung ist dem Processing in der ansteuernden Elektronik geschuldet ein weiterer Teil der Laufzeit des Schalls vom Lautsprecher zum Messmikro, das Signal selbst ist zu 100% identisch. Nehmen wir an die Gesamtverzögerung beträgt 10ms und der Teil der Elektronik beträgt 3ms, der akustische 7ms. Können wir diese Verzögerung bzw. konstante Gruppenlaufzeit mit dem Phasenwinkel beschreiben? Die Antwort ist NEIN. Wie bei dem oberen Beispiel können wir lediglich die Verzögerungszeit nehmen und in einen Phasenwinkel bei einer Frequenz X umrechnen, z.B. beträgt die Verzögerung 10ms, was 360° bzw. der Periodendauer von 100Hz entspricht, 10ms sind aber auch 180° bei 50Hz bzw. eine halbe Periodendauer usw. das ganze kann man für jede beliebige Frequenz ad absurdum führen …und genau das macht auch die Anzeige des Phasenfrequenzgangs unseres zweikanaligen Messystems. Erst wenn wir den Referenzkanal um die exakte gemessene Verzögerungszeit virtuell verzögern zeigt uns der Phasenfrequenzgang eine saubere Grade Linie auf 0° über das gesamte Frequenzspektrum was der konstruierten Realität entspricht.
ACHTUNG OFF TOPIC
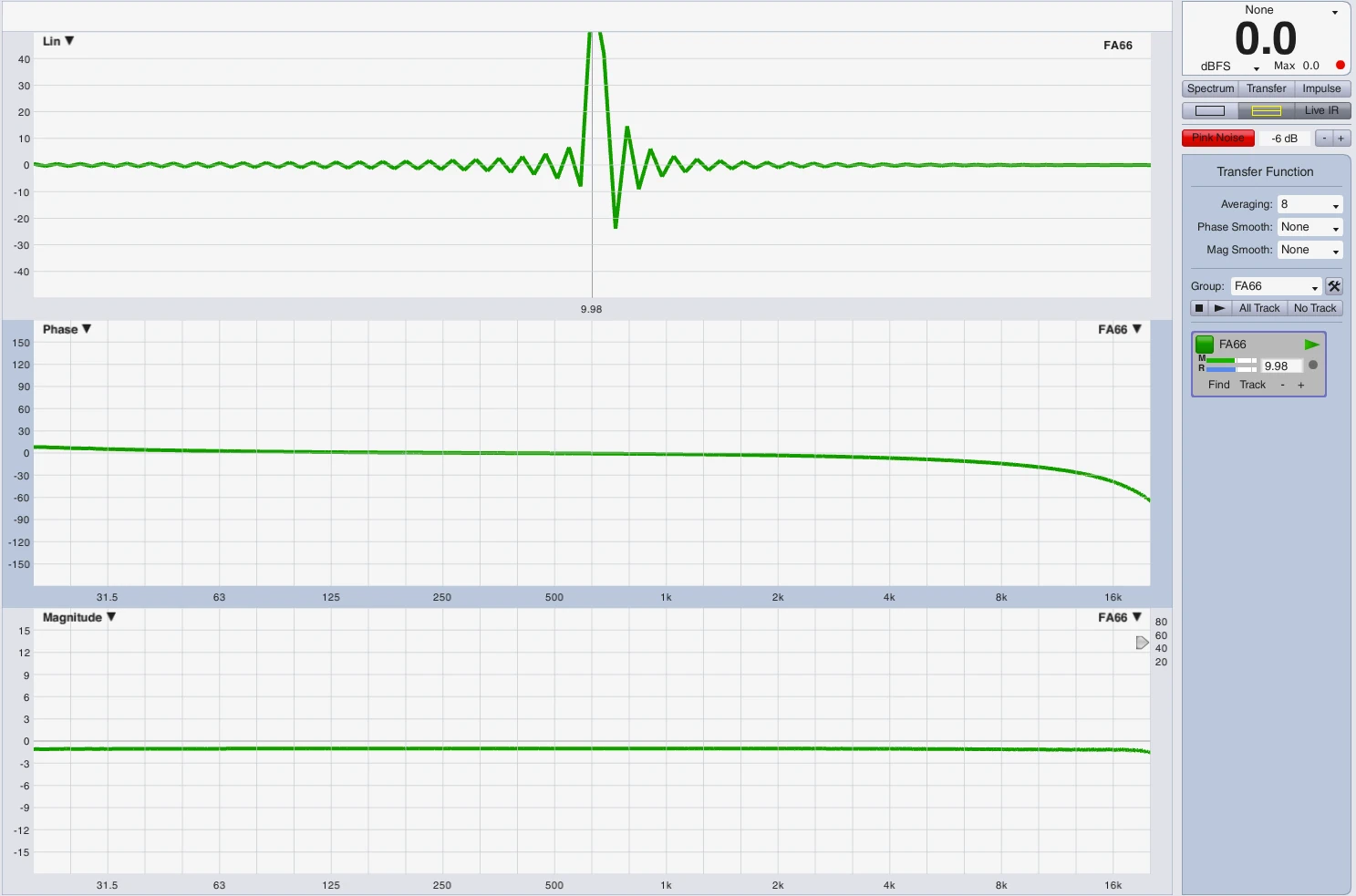
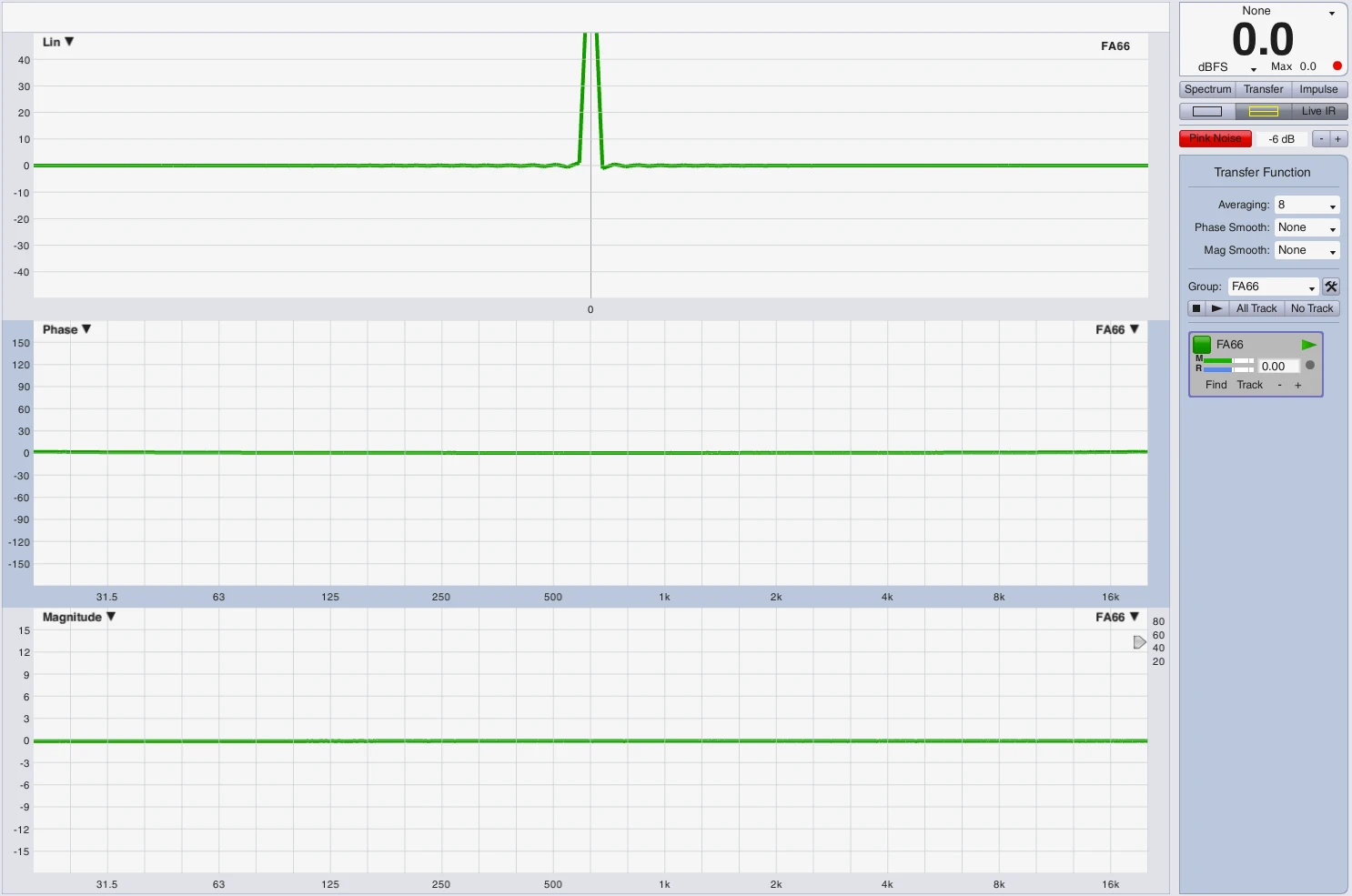
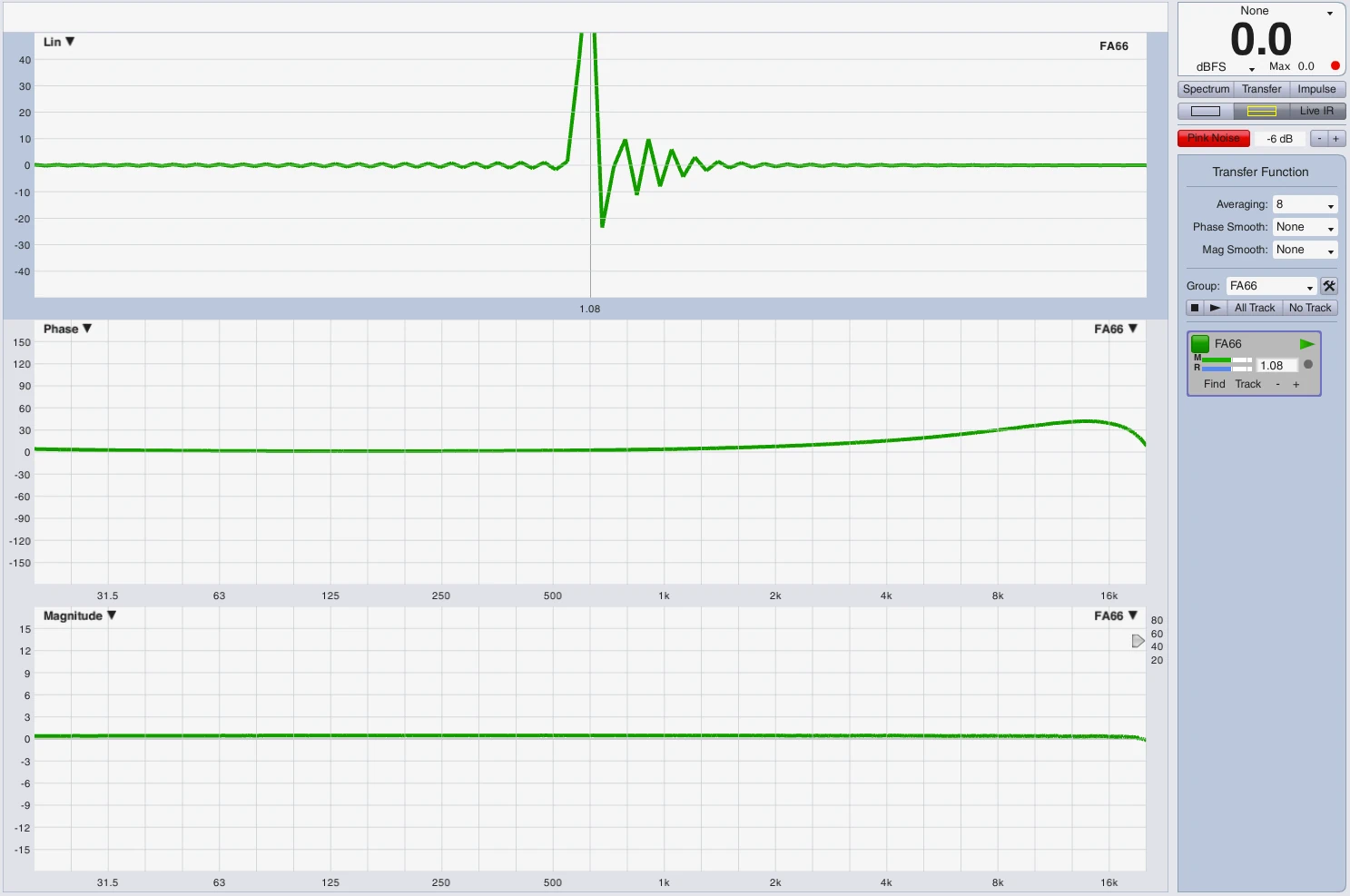
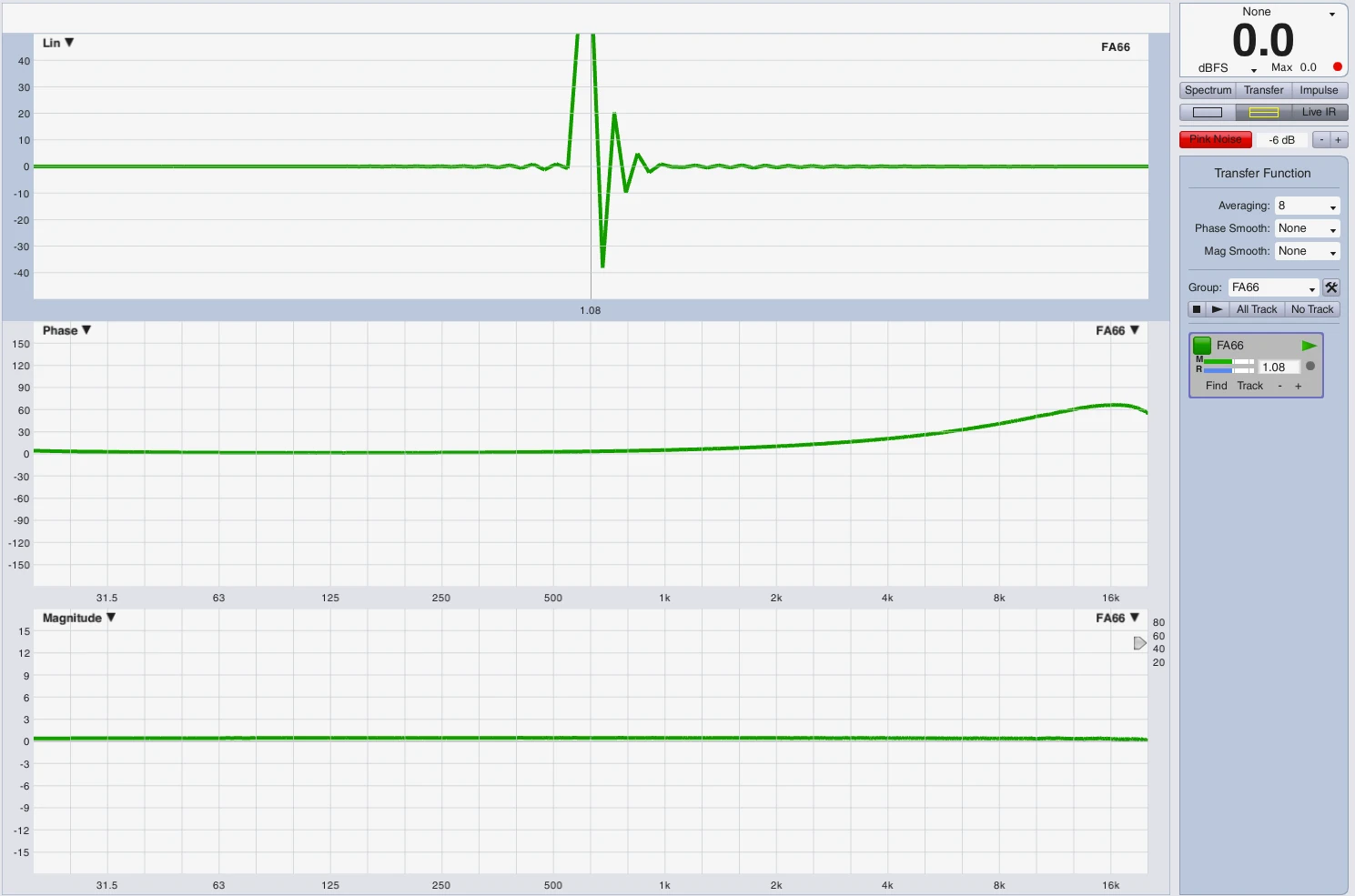
Impuls Darstellung auf der Zeitachse
Um die Hüllkurve bzw. den Signalzerfluß darzustellen habe ich folgenden Versuchsaufbau durchgeführt. Ein LM44 hat in Modul A den oben gezeigten Subweg mit HPF bei 25Hz und LPF bei 100Hz jeweils 24dB Butterworth. Das Modul B ist flat. In Logic habe ich einen 25Hz Sinus erstellt und einen 100Hz Sinus. Beide Regionen habe ich auf die Länge einer Periodendauer bei 25Hz getrimmt. Beide Signale (25Hz+100Hz) verlassen Logic über Ausgang 1 per DVS (…alles auf 96kHz) in LM44 Modul A+B und kommen ebenfalls via DVS in Eingang 1 + 2 wieder zurück. Eingang 1 = Modul A mit Sub Processing, Eingang 2 = Modul B ohne Filter. Da man bedenken muss, dass eine Mischung aus 2 Sinussignalen sofort eine Addition und ein neues komplexes Signal erzeugt und mir leider grade die Zeit fehlt ein optimales Frequenzverhältnis zu bestimmen habe ich 3 Aufnahmen erstellt, jeweils über Modul A und Modul B. Das Frequenzgemisch, 25Hz solo, 100Hz solo.
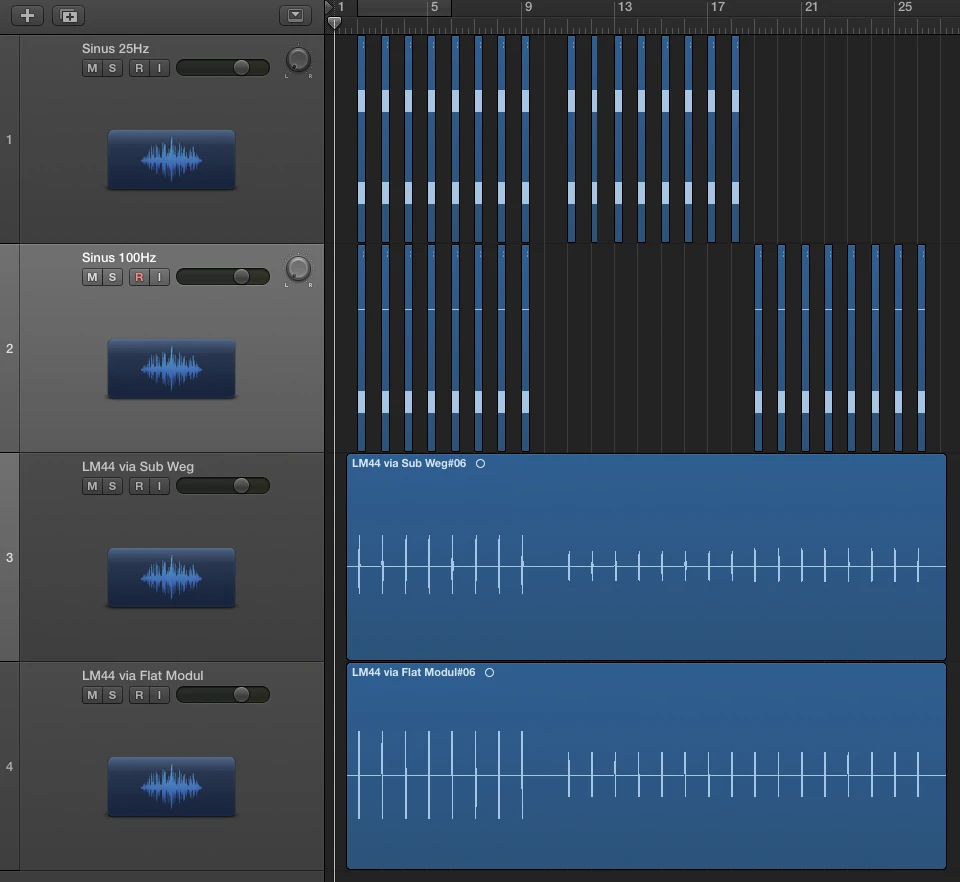
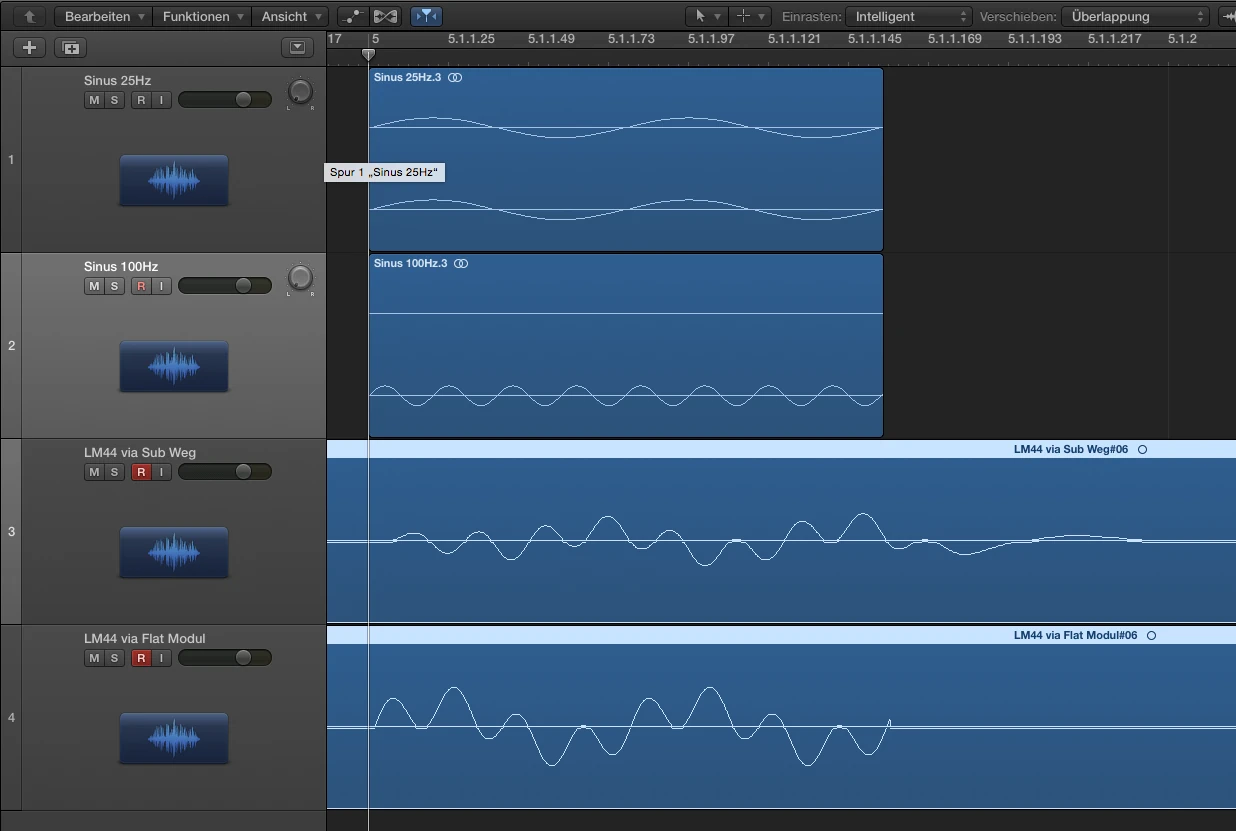
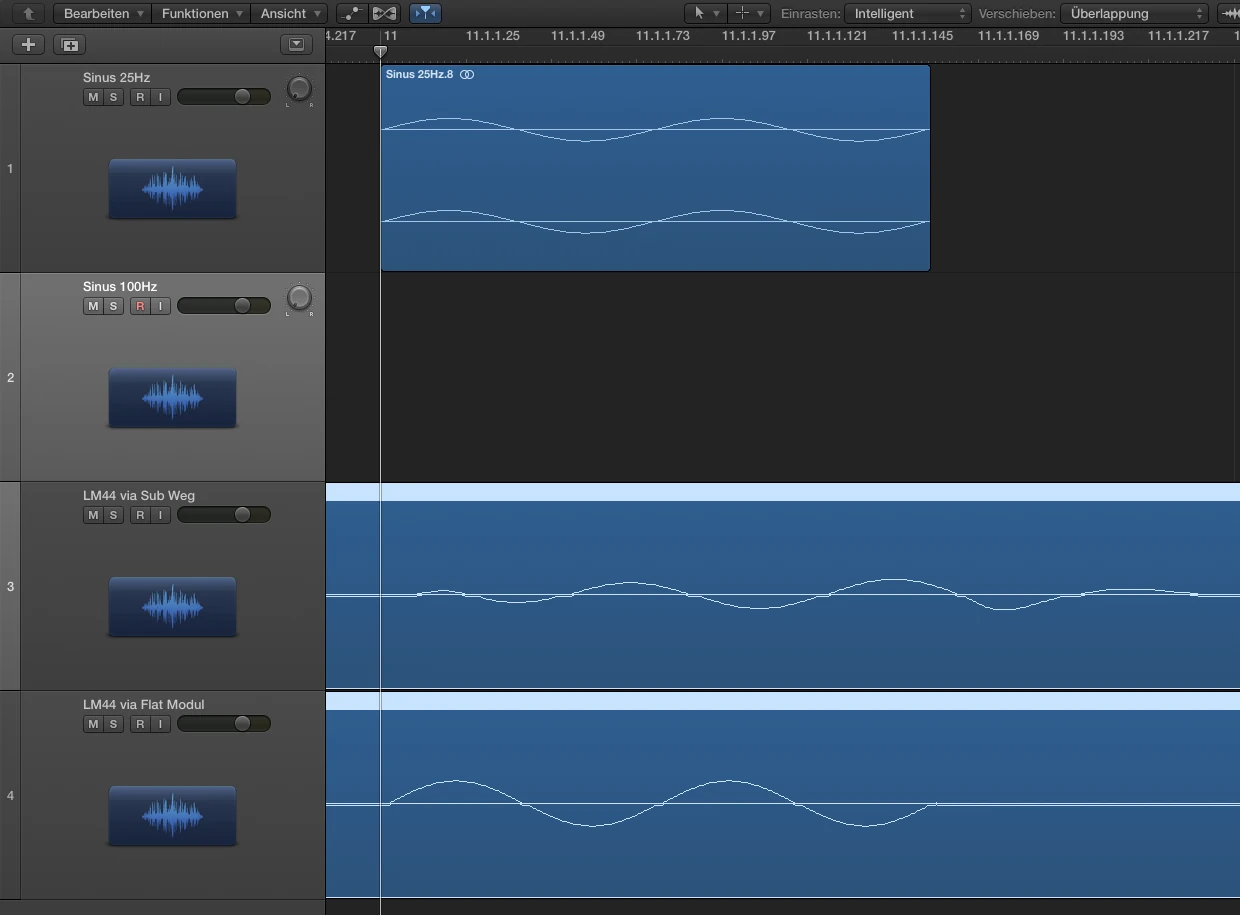
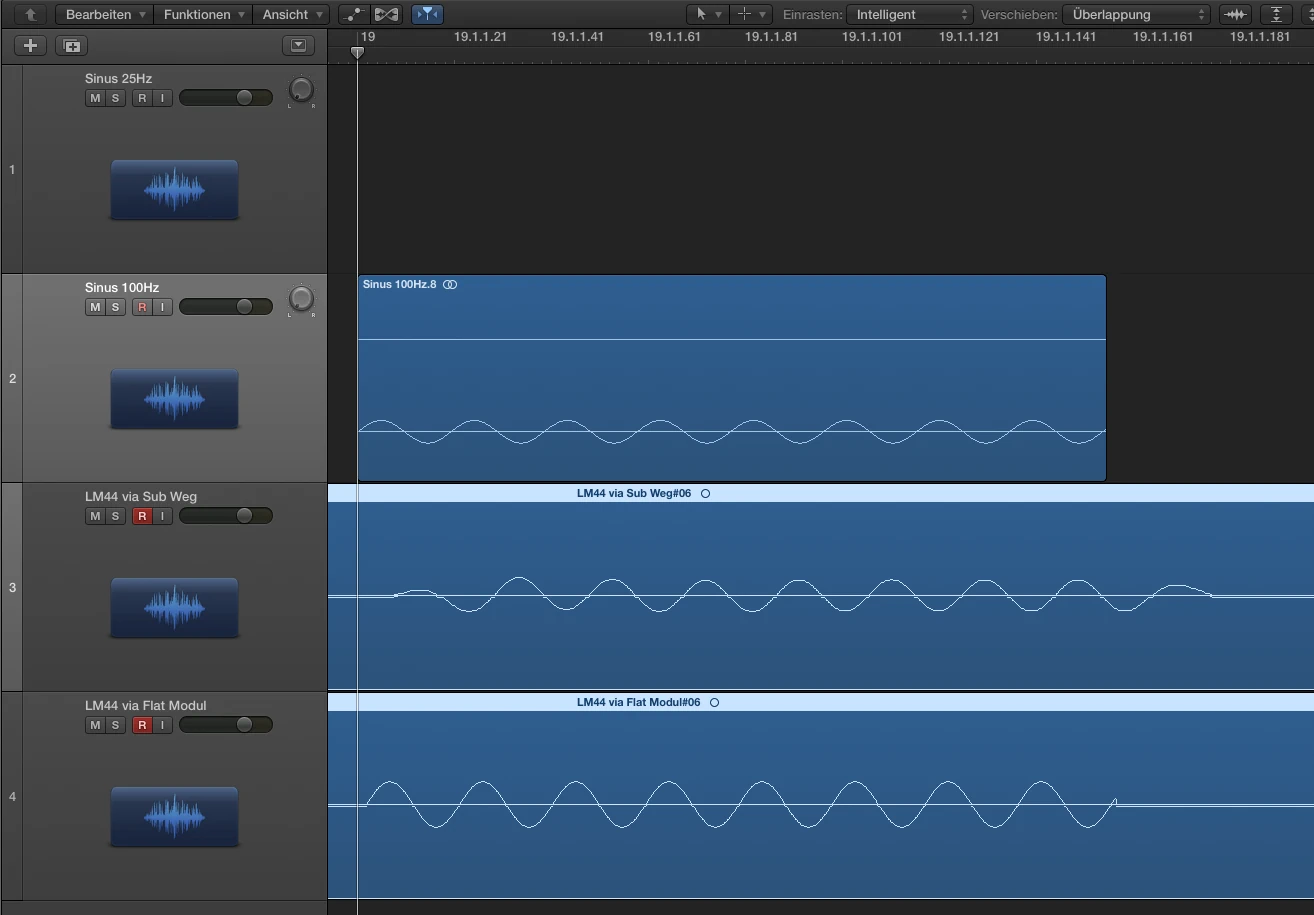
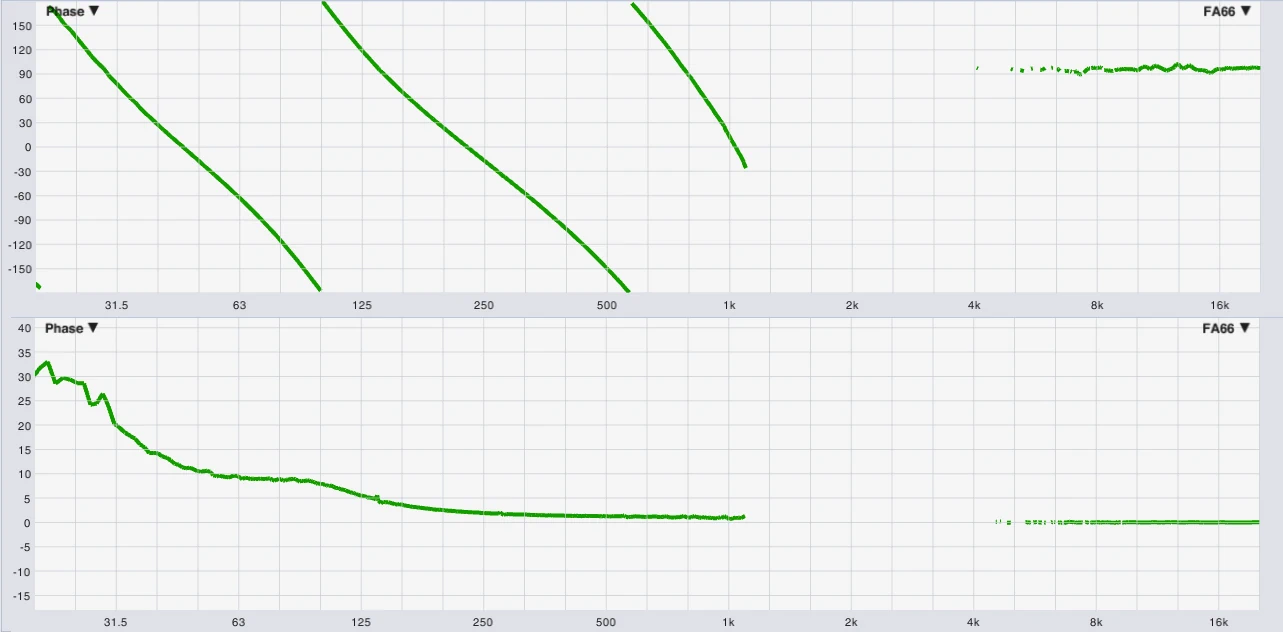
Die Gruppenlaufzeit ist höher als die der Quelle,
aber kleiner als die bei 25Hz, s.h. Smaart Messung.
FAZIT
1. Die Gruppenlaufzeit beschreibt das frequenzabhängige Laufzeitverhalten eines Übertragungssystems durch das ein bandbegrenztes Signal vollständig passiert.
(Bandbegrenzt kann natürlich auch 20Hz bis 20kHz bedeuten, oder 50Hz mit Bandbreite X wobei das System selbst auch stets eine Bandbreite aufweist und die Betrachtung nur durch das durchlaufende Signal = Sinus weiter eingegrenzt werden kann. Dies kann natürlich auch umgekehrt mittels FFT Messtechnik passieren)
2. Die Gruppenlaufzeit kann konstant und damit für alle Frequenzen gleich sein. Sie entspricht so einer einfachen Signalverzögerung (Delay).
3. Ist die Gruppenlaufzeit nicht konstant, entspricht dies einer Verzerrung des Phasenfrequezgangs. Einzelne Frequenzen des Übertragungsbandes weisen eine längere Laufzeit durch das System auf als andere. In dem Fall zerfließt die Hüllkurve des passierenden Signals, die Gesamtlaufzeit der betrachteten Frequenzgruppe beginnt und endet mit der ersten bzw. letzten Änderung der Amplitude. (d.h. der Amplitudenverlauf über die Zeit wird gezogen)
4. Die Bezeichnung “frequenzabhängiges Delay” trifft zwar irgendwie zu, ist aber aus oben genannten Gründen, aus meiner Sicht nicht hinreichend. Wenn man eine Messung betrachtet würde man in der Ansicht des Phasenfrequenzgangs mit Winkelachse in Grad sagen, die Phasenverschiebung bei X Hz beträgt X Grad, was umgerechnet Y ms bei der betrachteten Frequenz entspricht. Schaltet man die Darstellung auf Gruppenlaufzeit um, sehen wir direkt die Gruppenlaufzeit bei X Hz in Y ms. Da das System i.d.R. immer eine nicht konstante Gruppenlaufzeit aufweist, von FIR optimierten Topteilen mal abgesehen, macht es Sinn direkt das Wort Gruppenlaufzeit zu verwenden, z.B. die Gruppenlaufzeit bei X Hz beträgt Y ms.
Ich hoffe ich konnte mit meinem Beitrag ein bisschen Klarheit in das Thema Phase und Gruppenlaufzeit bringen und freue mich über konstruktive Diskussionen zu dem spannenden Thema. In einem folgenden aufbauenden Beitrag könnte ich mich mit dem Thema Allpassfilter als Alternative zum Delay bei der Einrichtung von Beschallungsanlagen auseinandersetzen. Diese immer populärer werdende Methode kann unbedingt Sinn machen, wenn man damit die Verzerrung der Phasenfrequenzgangs des Beschallungssystems optimiert. Sie kann jedoch auch nach hinten losgehen, wenn man genau das Gegenteil erreicht. Meine Hypothese lautet “Interessant, aber kein Allheilmittel das man blind bevorzugen sollte”.
Links & Dank
Mein Dank geht an Anselm Goertz, der im Production Partner 01/2017 das Thema zuerst aufgriff und damit wahrscheinlich halb Deutschland vor den Kopf stieß, die übliche Denkweise mal zu hinterfragen …was er zumindest bei mir geschafft hat. Allerdings erst nach dem Michael Häck eine Diskussion mit einer ketzerischen Frage startete, die bei mir üblicherweise zu einem schlaflosen Wochenende führt, bis ich die Nuss geknackt habe. Markus Zehner inspirierte mich das Thema Phase von vorne anzugehen und genauer über die Grundlagen nachzudenken, Merlijn van Veen danke ich für seine akribische Aufarbeitung von Beispielen, die mich inspirierten meine eigenen Ableitungen zu führen. Einig sind wir uns nur in einem Punkt den Markus treffend formuliert hat “je länger ich über das Problem nachdenke desto weniger sicher bin ich das ich es überhaupt verstanden habe” In diesem Sinne ist kritisches Hinterfragen erwünscht und Vorschläge zur Korrektur willkommen.